kimgusxo 님의 블로그
재귀(Recursion) 본문
1. 재귀(Recursion)란
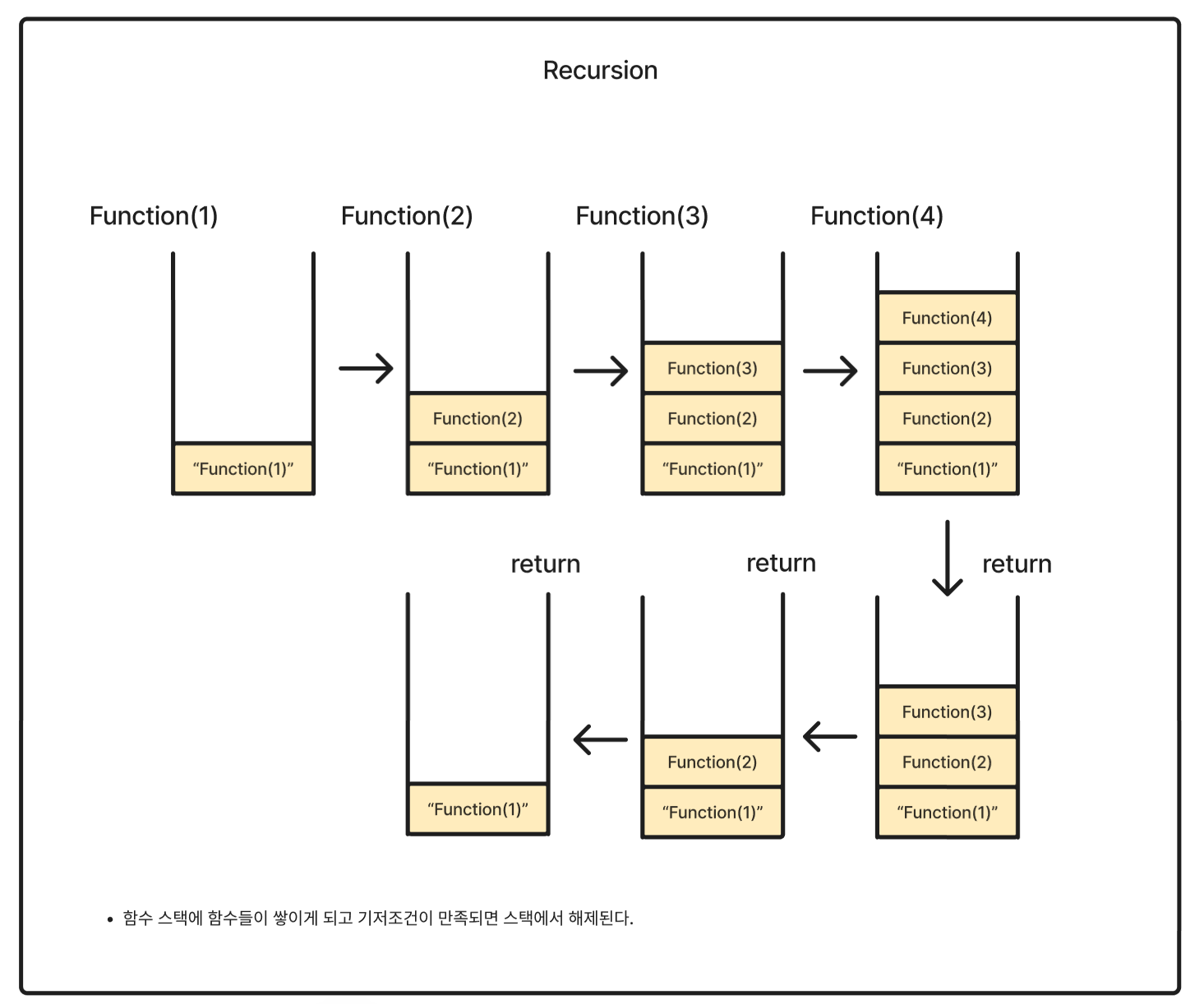
- 재귀는 함수가 자기 자신을 호출하는 기법이다.
- 문제를 여러개의 하위 문제로 분할하여 하위 문제를 해결한 후 이를 종합하여 전체 문제를 해결하는 방식
- DFS, 백트래킹, 트리순회, 피보나치 수열 등의 알고리즘으로 활용된다.
1-1. 핵심 아이디어
- 기저 조건(Base Case): 재귀호출이 무한히 반복되지 않고 종료되도록 하는 조건
- 재귀 호출(Recursive Call): 함수가 자기 자신을 호출하여 하위 문제를 해결하는 부분
2. 재귀의 장단점
- 장점: 문제 분할에 적합하고 반복문보다 간결한 코드로 표현할 수 있다.
- 단점: 재귀 호출마다 함수가 스택에 쌓이므로 메모리 사용이 크고 동일한 문제를 여러 번 계산할 경우 성능 저하가 발생한다.
3. 활용 알고리즘
3-1. 팩토리얼 계산
- n! = n(n-1)! 의 재귀적 정의를 사용한다, 0!=1인 기저조건을 사용한다.
public class FactorialExample {
public static long factorial(int n) {
// 기저 조건
if(n == 0) {
return 1;
}
// 재귀 호출
return n * factorial(n-1);
}
public static void main(String[] args) {
// 예제 데이터
int number = 5;
System.out.println(factorial(number)); // 출력: 120
}
}
3-2. 피보나치 수열
- F(n) = F(n-1)+F(n-2)의 재귀적 정의를 사용한다. F(0)=0, F(1)=1인 기저조건을 사용한다.
public class FibonacciExample {
public static int fibonacci(int n) {
// 기저 조건
if(n <= 1) {
return n;
}
// 재귀 호출
return fibonacci(n-1) + fibonacci(n-2);
}
public static void main(String[] args) {
// 예제 데이터
int index = 10;
System.out.println(fibonacci(10)); // 출력: 55
}
}'Algorithm' 카테고리의 다른 글
| 이분 탐색(Binary Search) (0) | 2025.02.28 |
|---|---|
| 브루트포스(Brute Force) (0) | 2025.02.27 |
| 셋(Set) (0) | 2025.02.24 |
| 맵(Map) (1) | 2025.02.23 |
| 트리(Tree) (0) | 2025.02.21 |



